물론 예외는 있겠지만, 자료구조와 알고리즘의 올바른 선택은 좋은 프로그램의 중요한 요소임에 틀림없다. 오늘 포스팅에서는 프로그램을 짤 때 어떤 자료구조를 선택해야하는가를 간략히 정리해볼까 한다. 자료구조 클래스는 주로 ATL 컬렉션 클래스에 있는 CAtl* 클래스를 중심으로 얘기할 것이다. 그러나 자바나 다른 언어의 경우에도 비슷하게 적용할 수 있을 것이다.프로그램(Program) = 자료구조(Data Structure) + 알고리즘(Algorith)
나는 STL을 솔직히 많이 사용하지 않는다. STL의 강력한 점은 알고리즘을 쉽게 적용할 수 있다는 것이다. 그런데 굳이 STL이 MFC 혹은 ATL에서 제공하는 템플릿 라이브러리에 비해 더 빠른 처리 속도를 주거나 더 적은 메모리를 쓰는 것이 아니다. 또한, predicate와 같이 각종 템플릿 타입에 대한 행동 정의 (예를 들어, 크기를 비교하거나 해쉬 값을 만들거나)도 ATL Collection Library에서는 무척 직관적이고 사용하기 쉬워졌다. 따라서 나는 ATL 라이브러리를 애용한다.
MFC 유저들은 흔히 CArray, CList, CMap으로 대표되는 MFC 컬렉션 클래스들을 많이 쓸 것이다. MFC 내부에도 저 자료구조는 광범위하게 사용된다. 그러나 Visual Studio .NET, MFC 버전 7부터, ATL 컬렉션 클래스가 플랫폼 독립적으로 지원되고 있다. 또한 CString 또한 MFC 의존 없이
#include <atlstr.h>로 언제든지 사용할 수 있다. 따라서 MFC를 쓰지 않은 경우에도 ATL 컬렉션 라이브러리와 CString을 얼마든지 사용할 수 있다.그럼 이제 본론으로 들어가서 자료구조 선택에 대한 가이드라인을 생각해보자. 전산학을 전공한 사람에겐 기초적인 내용이지만 의외로 배열과 리스트의 차이점, 해쉬 테이블과 이진 트리와의 차이점을 잘 모르는 개발자들이 많아서 조금이나마 도움이 될까해서 요렇게 남긴다.
1. Array - CAtlArray, CArray, std::vector
C언어에서 지원하는 배열과 똑같은 문법으로 사용할 수 있는 말그대로 배열이다. 단, 그 크기가 동적으로 변할 수 있다. C언어의 배열과 같이 operator[]로 접근이 가능하다. 즉, random access가 가능하다. 가장 가벼운 오버헤드를 가지고 있고, 단순한 자료 저장은 최대한 배열을 사용해야한다.
- 삽입/삭제: 배열 끝에서의 추가 및 삭제는 상수 시간 O(1). 그러나 그 외의 원소를 삽입/삭제 할 경우에는 O(n)의 시간이 걸린다. 여기서 잠깐 알고리즘 수행 시간(time complexity)을 나타내는데 쓰이는 Big-Oh notation에 대해서 알아보자:
- 검색: 일반적인 경우에는 O(n). 만약 원소들이 정렬이 되어있다면 O(log n)가 가능하다.- O(1): 현재 배열의 크기와 상관없이 언제나 같은 시간이 걸린다는 뜻이다. 배열 마지막에 새로운 원소를 넣는 작업의 경우, 배열의 크기를 알고 있기 때문에 for 순환 없이 바로 작업을 수행할 수 있다.
- O(n): 주어진 작업을 완료하기 위해서는 최악의 경우, 현재 배열의 길이만큼 탐색을 해야한다. 정렬되지 않은 배열에서 특정 원소를 찾는 것은 최악의 경우 모든 원소를 다 뒤져 봐야하므로 배열의 길이에 비례하는 시간이 걸린다.
- O(log n): 만약 배열의 원소들이 정렬이 되어있다면 이진탐색기법을 활용할 수 있다. 이 경우 연산 회수가 길이의 로그에 비례함을 알 수 있다. 왜냐면 한 번 수행할 때 마다 탐색해야할 데이터의 크기가 반으로 줄기 때문이다. 정확하게는 base가 2인 로그이지만 흔히 log로 표현한다. (밑이 10인 상용로그나 e인 자연로그는 아님을 주의)
2. Double Linked List - CAtlList, CList, std::list
설명이 필요없는 자료구조론의 교본; 더블 링크드 리스트. 배열과의 가장 다른 점은 원소가 연속적인 메모리가 아닌 포인터로 불연속적으로 저장된다는 점이다. 따라서 랜덤하게 접근이 불가능하며, ATL/MFC의 경우에는 POSITION이라는 iterator를, STL에서는 list::iterator 객체를 이용해서 접근해야한다. (따라서 STL의 소팅 알고리즘을 바로 적용할 수 없다. 소팅 알고리즘은 random access iterator를 요구하기 때문이다.)
- 삽입/삭제: 삽입을 하려면 앞/뒤의 노드에 대한 iterator가 필요하다. 따라서 이것을 구했다면 삽입은 상수시간 O(1)에 가능하다. 그러나 마치 배열 처럼 "몇 번째"에 넣기 위해서는 그에 해당하는 iterator를 구해야하고 결국 O(n)이 걸리게 된다. 따라서 이와 같은 경우가 많다면 배열을 사용해야 한다. 나의 경험상, 생각보다 더블 링크드 리스트가 반드시 필요한 경우는 많지 않았다.
- 검색: 당연히 O(n)
* 이 쯤에서 자료구조론 책에는 큐도 나오고, 스택도 나오고, deque도 나오지만 앞에 언급한 자료구조를 응용한 것에 불과하다.
3. Hash Table - CAtlMap, CMap, std::hash_map
해쉬 테이블은 key와 value 쌍을 저장하는 자료구조로서 DB의 기초가 되는 매우 중요한 자료구조이다. 해쉬 테이블의 개략적인 구조는 아래 그림과 같다. (구글에서 찾은 그림)
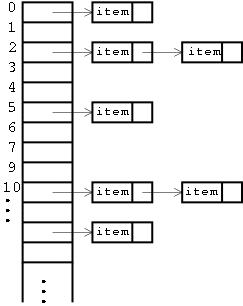

검색과 삭제의 방법도 같다. 주어진 키의 해쉬 값을 계산 한 뒤, 원하는 버킷으로 찾아가서, 버킷에 달려있는 데이터 노드와 비교를 하여 (선형 탐색) 원하는 데이터를 찾는 것이다.
따라서 검색에 필요한 시간 중 버킷까지 찾아가는 시간은 해쉬 테이블의 크기가 얼마가 되었든 동일하다. 그러나 만약 해쉬 테이블에 너무 많은 데이터가 있어 충돌이 많이 일어난 경우, 즉, 버킷에 긴 리스트가 달려있는 경우에는, 탐색하는데 시간이 소요되게 된다.
이론적인 해쉬 테이블의 검색 속도는 O(1+n/m)으로 표현한다. 여기서 m은 slot의 개수, n은 원소의 개수로 n/m은 흔히 load factor로 표현이 된다. DB는 잘 몰라서 그런데, 흔히 0.7 ~ 1.2 정도의 값을 가지는 것이 좋을 것이다. 그러나 리스트는 평균적으로 그렇게 길지 않으므로 흔히 탐색은 상수시간 O(1)이 걸린다고 말한다. (정말로 최악의 경우에 모든 키의 해쉬 값이 하나로만 나온다면 검색 속도는 리스트와 같아진다.)
추가 및 삭제도 모두 상수시간 O(1)이 걸린다. 그림과 같이 주어진 이름으로 전화번호를 찾아야하는 사전과 같은 구조에서는 해쉬 테이블이 가장 좋다.
그러나 하나 주의해야할 것은, 해쉬 테이블에 저장된 데이터는 순서를 예측할 수 없다. 그림에서 해쉬 테이블에 저장된 모든 데이터를 출력한다고 할 때, 이는 정렬되지 않은 값이다. 왜냐면 주어진 키의 해쉬 값에 따라 정렬이 되는데 이는 일반적으로 예측할 수 없기 때문이다. 따라서 위의 그림에서 사람 이름으로 정렬해서 출력하고 싶다면, 어쩔 수 없이 모든 데이터를 한번 정려를 해야한다.
4. Balanced Binary Search Tree(Red-Black Tree) - CRBMap, std::map (MFC 컬렉션은 없음)
역시 매우 중요한 자료구조. 균형잡힌(!) 이진 탐색 트리는 추가, 삭제, 검색을 모두 로그 시간 O(log n)에 수행할 수 있는 매우 우수한 자료구조이다. 비록 해쉬 테이블 상수 시간에 이루어지지는 않지만, 탐색 트리의 장점은 키 값들이 정렬이 되어있다는 것이다. 따라서 위의 전화번호부 예에서 사람 이름에 대해서 소팅을 많이 해야한다면, 이진 트리를 사용해야한다.
이진 트리는 아래와 같이 생긴 자료구조이다. 그러나 최악의 경우 모든 원소가 한 쪽에만 달려있다면, 이는 리스트와 전혀 다름이 없다.


반면, AVL Tree라고 불리는 녀석은 양쪽 노드의 길이가 최대 하나 밖에 차이가 나지 않도록 한다. 훨씬 더 빡세게 균형을 맞춘다. 따라서 당연히 이 균형을 맞추는 보정 작업에 소요되는 시간이 Red-Black Tree보다 크다.
키와 데이터 쌍을 저장할 때, 검색이 가장 우선 순위라면 당연히 해쉬 테이블을 써야한다. 그러나 이 키 값들이 정렬이 되고 싶다면 Red-Black Tree가 가장 좋은 자료구조이다.
정리
위의 모든 내용을 정리한 아주 좋은 테이블이 MSDN 싸이트에 있다.
|
Shape |
Ordered? |
Indexed? |
Insert an element |
Search for specified element |
Duplicate elements? |
|
List |
Yes |
No |
Fast (constant time) |
Slow O(n) |
Yes |
|
Array |
Yes |
By int (constant time) |
Slow O(n) except if inserting at end, in which case constant time |
Slow O(n) |
Yes |
|
Map |
No |
By key (constant time) |
Fast (constant time) |
Fast (constant time) |
No (keys) Yes (values) |
|
Red-Black Map |
Yes (by key) |
By key O(log n) |
Fast O(log n) |
Fast O(log n) |
No |
|
Red-Black Multimap |
Yes (by key) |
By key O(log n) (multiple values per key) |
Fast O(log n) |
Fast O(log n) |
Yes (multiple values per key) |
* 혹시 작성한 내용 중 틀린 부분이 있으면 꼭 지적 해주세요.
